What is NOT STEERING

• What you see in the movies
• Not big crowds of ambient/stationary people

MiArmy in Maya

I've fallen, and I can't get up! from Dave Fothergill vfx on Vimeo.

What is steering

• Situationally aware agent (locally)
• Active collision avoidance
• Has a GOAL (target location)

Hitman: Absolution

Uses Boids algorithm [Craig W. Reynolds, 1987]

Steering Model

1. Sliding particle
2. Configuration state \(q = \langle x, y, \dot{x}, \dot{y} \rangle \)
3. Commonly internal to the steering model
1. Preferred Velocity \(v_{pref}\)
2. max speed \(v_{max}\)
3. radius \(r\)
4. neighbours \(a_{0} \ldots a_{n}\)
5. waypoints \(p_{0} \ldots p_{m}\)

Simulation loop?

1. Steering decision can be even simpler than simulation loop
2. \(\langle x, y, \dot{x}, \dot{y} \rangle' = steeringAlgorithm(\langle x, y, \dot{x}, \dot{y} \rangle, \Delta t)\)

Assume steering algorithm has access to all other agents

Social Forces / HIDAC

• Obstacle repulsion forces

[Helbing et al. 2000, Pelechano et al. 2007]

Agent repulsion force

Net force

Agent Comfort zone

• Repulsive when agents almost collide

Social Forces Demo?

Continuum crowds

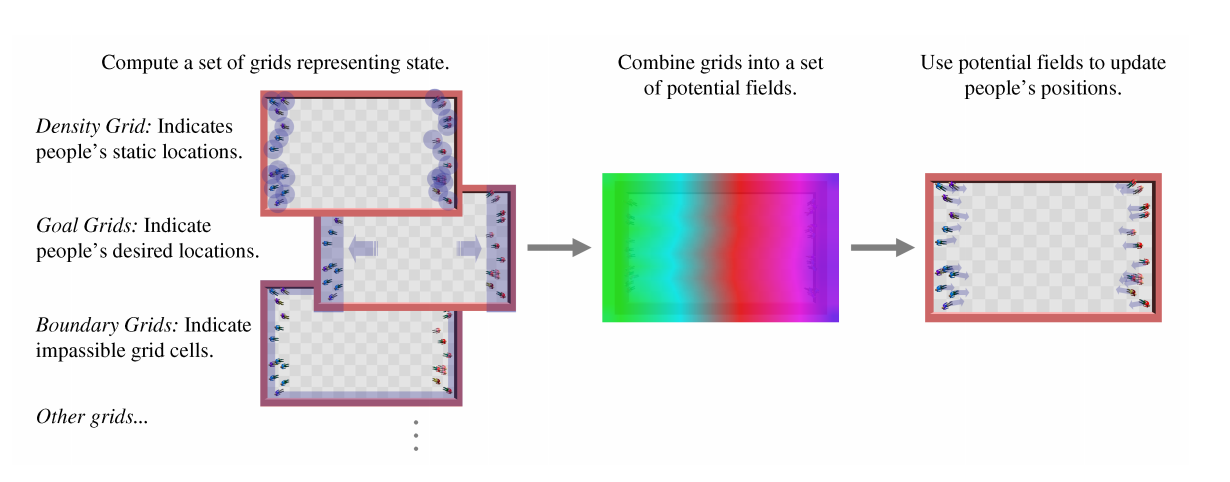
[Treuille et al. 2006]

Key ideas

• Convert the crowd to a density field
• For each group:
• Construct the unit cost field C
• Construct the potential φ and it’s gradient ∇φ
• Update the agent locations
• Enforce the minimum distance between people

Continuum Crowds Demo?

Reciprical Velocity Obstacles (RVO)

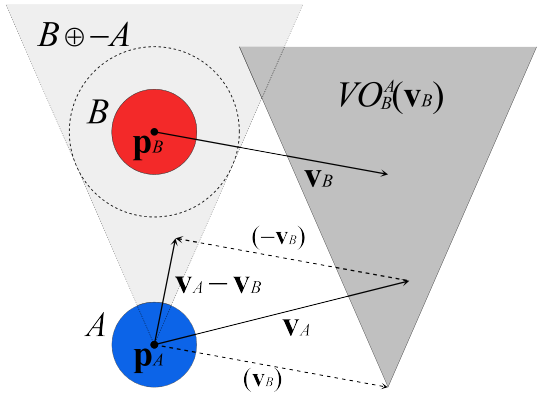
• Keep velocity outside of Velocity Obstacle

[van den Berg et al. 2008]

Smooth (RVO)

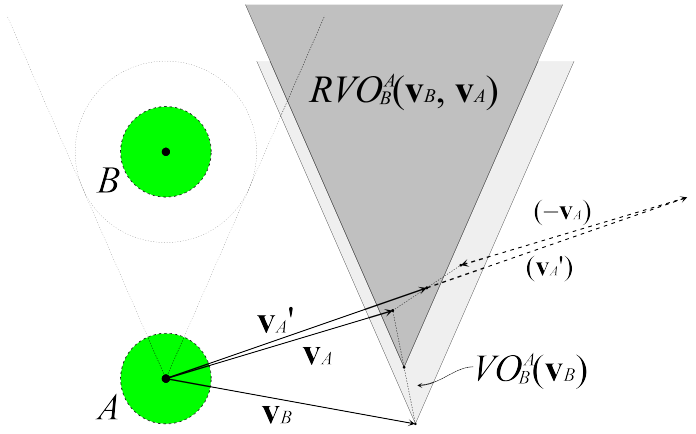
• Velocity is average of velocity outside of obstacle and desired.

Multi-agent descision (RVO)

• Choose best velocity outside of union on RVOs

RVO demo?

Plan, Predict, React (PPR)

Short term planning

[Singh et al. 2011]

Predict/Preceive

React

Demo

Issues with Disk model

1. Foot Skating
2. Does not capture rigid body
3. Limbs can intersect
4. People are not circular

Re-visit Hitam Absolution??

Footstep based [Singh et all 11]

[Singh et al. 2011]

video

Demo?

SteerBench

1. Suite of steering benchmarks
1. Consist of common steering benchmarks and new ones
2. 
2. set of metrics that are independant of steering approach
1. number of colissions
2. total acceleration, distance traveled, time spent and energy

[Singh et al. 2009]

ScenarioSpace: [Kapadia et al 11]

1. Construct a subspace of possible scenarios
2. What should this subspace consist of?
3. More difficult scenarios
• 
• Reference agent
• Force interaction
4. Better metrics for comparison
• Coverage
• Time quality
• Distance Quality

[Kapadia et al. 2011]

SteerFit: Steering algorithm parameter fitting

1. Each steering algorithm models the steering problem well
2. Each algorithm has a number of parameters
3. How do they affect the algorithms behaviour?
4. Can we improve the algorithms?

[Berseth et al. 2013]

Optimization framework

1. We optimize the parameters (\(v\)) of a steering algorithm (\(A_{v}\))
2. Over a test set \(T\) (representative set)
3. For a user defined objective \(ƒ\)
4. Important issue: do the optimized parameters generalize?

Behavioural Objectives

1. Deficiency \(d\): percentage of scenarios failed
2. Distance Quality \(q^{d}\): ratio of optimal distance to actual distance
3. Time quality \(q^{t}\): ratio of optimal time to actual time
4. Effort Quality \(q^{e}\): ratio of optimal bio-mechanical energy to actual [Guy et al. 10]
5. Computational Efficiency \(e\): ratio of max desired computational time to actual.

Formulate an optimization

• Normalize Metrics
• \(\mathbb{M} = \langle d, q^{d}, q^{t}, q^{e}, e \rangle\)
• Weighted sum
• \(f(A_{v},\textbf{w}) = \sum\limits_{m_{i} \in \mathbb{M} } w_{i} \cdot m_{i} , \sum\limits_{w_{i} \in \textbf{w}} w_{i} = 1\)
• Minimization
• \( \textbf{v}^{*}_{\textbf{w}} = \arg \min_{\textbf{v} \in \mathbb{V} } f(A_{v},\textbf{w})\)

SteerFit Findings

Relative percent improvement over default

Results

These Results are good but what do we really want?

• We want crowds to look like human crowds
• Ground Truth Similarity: Statistical similarity to recorded crowd data [Guy et al. 2012].

SteerFit Findings (Entropy)

Trade-offs between objectives

• For every set of weights we need to do an optimization?
• Can we compute a mapping from weights \(\mathbb{W}\) to parameters \(\mathbb{V}\)?

Adaptive Sampling vs Pareto Optimal

• Adaptive Sampling
• Uses weighted combinations of objectives
• Weighted combination is ad-hoc
• Does not optimize
• Pareto Optimal Front
• More principled method
• Computes trade-offs of multiple objectives

Pareto Efficiency

• Can’t improve one objective without reducing another
• Pareto Optimal Front
• Collection of Pareto Efficient points

Pareto Optimial Front

ORCA	Social Forces

• NGSA-II

Weight mapping

Pareto Optimial Front

More Results

Dicussion

• Optimize algorithms for combinations of objectives
• principled model of trade-offs between objectives

Architecture optimization

• Lets not optimize the crowd but the environment for the crowd
• Can we optimize parts of buildings for crowd flow?

[Berseth et al. 2015]

Parameterized scenario (Scenario Subspace)

• A scenario \( s \) is a set of Obstacle and Agents ( \(s = \langle \textbf{O},\textbf{A} \rangle \))
• An obstacle \( o \) has a position \( \textbf{x} \) and geometry (circle or square)
• An agent \( a \) has a position \( \textbf{x}\), radius \( r \) and goal location \( \textbf{g} \)
• A Scenario subspace will define bounds on positions (agents or obstacles) \( \mathcal{S}_{sub} \)
• A scenario is created from \( \mathcal{S}_{sub} \) with parameters \( \textbf{p} \in \mathcal{P} \)

Crowd Flow

• $$ f(\textbf{p}) = \frac{ | A_c | |A|}{\sum_{a \in A_c} t_a} $$
• \(A_{c}\), number of agents that completed the scenario
• \(t_{a}\), Time to complete scenario for agent \(a\)

Formulate Optimization

• penalize overlapping obstacles \(g(\textbf{p})\)
• \(g(\textbf{p}) = \sum\limits_{\forall (o_{1},o_{2}) \in O \times O } g_{o}(o_{1},o_{2}) \)
• $$ \textbf{p}^* = \arg \min_{\textbf{p} \in \mathcal{P}} (-f(\textbf{p}) + g(\textbf{p})) $$

Path planning

• Path planning influences \(v_{pref}\)
• Path planning is usually based on some static discretization of the environment
• This results in very bad noise in the optimization
• Jaring discountinuities in flow wrt \(\textbf{p}\)
• Increased crowd congestion

Flow analysis

ORCA	PPR	Social Forces

Results

optimization results